Postać ogólna jest najbardziej powszechna. Jest to postać będąca wielomianem stopnia drugiego, z czego wynika, że może posiadać maksymalnie dwa miejsca zerowe.
Jej wzór to:
f(x) = ax2 + bx + c gdzie a≠0
natomiast a, b i c są to współczynniki. Szczególnym współczynnikiem jest c zwany wyrazem wolnym.
Wykres funkcji kwadratowej to np.:
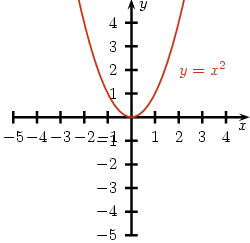
Jest to przykład wykresu, gdzie „b” i „c” równają się zero.
Charakteryzacja współczynników:
Współczynnik „a” odpowiada za dwie własności:
- Nachylenie ramion do osi OX:
- Im współczynnik „a” jest większy tym bardziej ramiona paraboli są skierowane ku osi OY.
- Im współczynnik „a” jest mniejszy tym bardziej ramiona paraboli są skierowane ku osi OX.
- Skierowanie ramion paraboli w górę lub w dół:
- Jeżeli „a” jest większe od zera (dodatnie) to ramiona paraboli są skierowane do góry.
- Jeżeli „a” jest mniejsze od zera (ujemne) to ramiona paraboli są skierowane w dół.
Współczynnik „b”:
- Jeżeli c = 0 to z przeciwnej wartości współczynnika „b” można odczytać miejsca zerowe, np.:
f(x) = x2 + 2x
Miejscami zerowymi są: 0 i -2.
Problem pojawia się, kiedy „c” jest różne od zera. Wtedy do obliczenia miejsc zerowych trzeba użyć wzorów. (Patrz: „Strona główna->Miejsca zerowe funkcji kwadratowej” lub „Postać iloczynowa”)
Współczynnik „c”:
- Wyznacza on punkt przecięcia się wykresu z osią OY, czyli jest on wartością funkcji dla argumentu równego zero.
